Satz von Weyl über Gleichverteilung

Der Satz von Weyl (nach Hermann Weyl) ist die Grundlage für arithmetische Zufallszahlengeneratoren. Er besagt:

Sei ${\displaystyle y_{0}\in \ ]0,1[}$ eine irrationale Zahl. Dann hat die Folge

${\displaystyle (u_{i})_{i\geq 1}\subseteq \ ]0,1[}$,

gliedweise definiert durch

${\displaystyle u_{i}=iy_{0}-\lfloor iy_{0}\rfloor =iy_{0}\ {\bmod {\ }}1}$

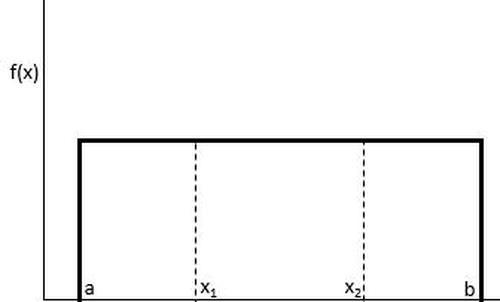
die asymptotische Gleichverteilungseigenschaft. Für alle ${\displaystyle a,b\in \mathbb {R} }$ mit ${\displaystyle 0$ gilt also:

${\displaystyle {\frac {\left|\{i|1\leq i\leq n;a\leq u_{i}\leq b\}\right|}{n}}\quad {\xrightarrow[{n\rightarrow \infty }]{\quad }}\quad b-a}$.

Anders gesagt: die Wahrscheinlichkeit, dass ein willkürlich gewähltes Folgenglied in ${\displaystyle [a,b]}$ liegt, beträgt ${\displaystyle b-a}$.